Hybrid FEM/SEA

Is hybrid FEM/SEA solving the mid-frequency problem?

A real technical system consists of hundreds of different subsystems. They have different wave fields of completely different wave speed and nature. In addition the size of each subsystem is also varying.

The conversion from deterministic (FEM) to random (SEA) subsystem occurs with increasing frequency. Thus, it happens – mainly in mid-frequency – that there are subsystems that are still deterministic whereas others are already random. In this case both methods are required at the same time in one model. The method that solves this issue is called the hybrid FEM/SEA method and was established by Phil Shorter and Robin Langley.

The hybrid FEM/SEA method not only solves the mid-frequency problem, it also establishes a excellent and straight-forward approach to develop the SEA theory in detail.

Developing the theory means on the one hand, to describe the impact of the SEA systems to the FEM subsystems, and to consider the impact of the FEM subsystems in the SEA subsystems. The first item means that the connected SEA subsystems change the matrix and the load of the deterministic FEM equation. The second item leads to changes in the SEA matrix due to the FEM systems.

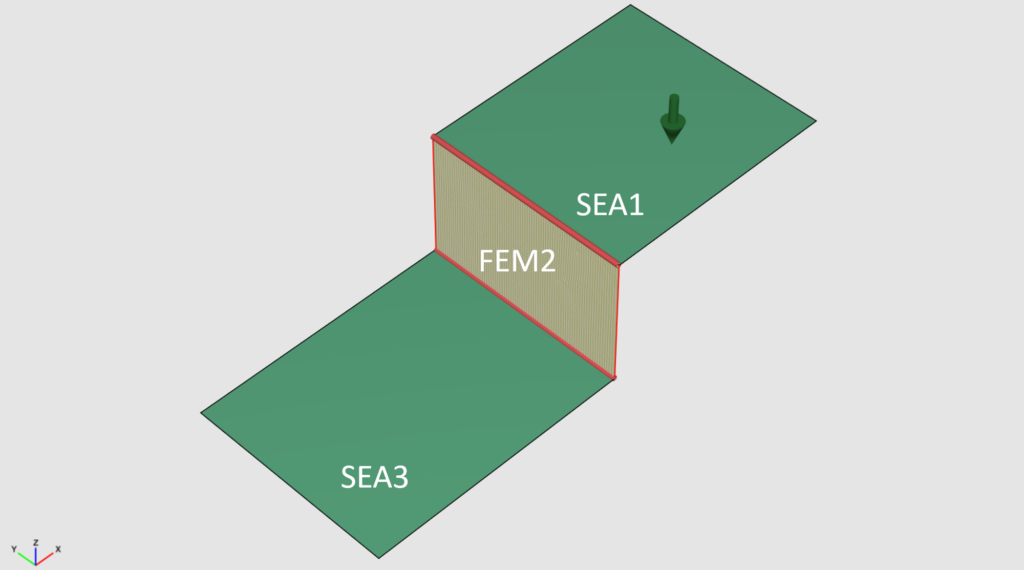
A typical hybrid method problem

Imagine that the center plate is stiff and has much lesser modes than the first and third plate. In this case plate 1 and 3 become random, but plate three is still deterministic. So we have the situation that the best suited method for plate 1/3 is the statistical energy analysis method, but the plate 2 must still be modeled using deterministic methods.

Sketch of Hybrid FEM/SEA model denting the center FEM plate by colored mode shape — **Figure:** Hybrid FEM/SEA model with deterministic shape of center FEM system

This means, that SEA systems 1 and 3 are connected by an FEM subsystem. This requires the definition of hybrid junctions that connect the SEA to the FEM systems. In the following the result of a pure SEA model and the hybrid FEM/SEA model are compared to the (reference) FEM solution.

Figure: FEM Frequency response compared to pure SEA and hybrid FEM/SEA solution

We can see that plate 2 is well predicted by the hybrid FEM/SEA approach but the SEA result is overestimating the velocity. When it comes to plate 3 the SEA result is simply wrong. But the hybrid model results cope well with the reference solution.

The hybrid theory is explained in chapter 7 of the book and applied to simple examples in chapter 11.

Chapter 12 provides practical industrial cases using hybrid methods. The chapter goes through all the comprising steps hybrid FEM/SEA modeling. The results are compared to the pure SEA results showing again the range of validity for SEA simulation.

In pyva there are fully worked out examples presenting a twin reverberation chamber with both rooms modeled as random cavities and the plate modeled as FEM subsystem.

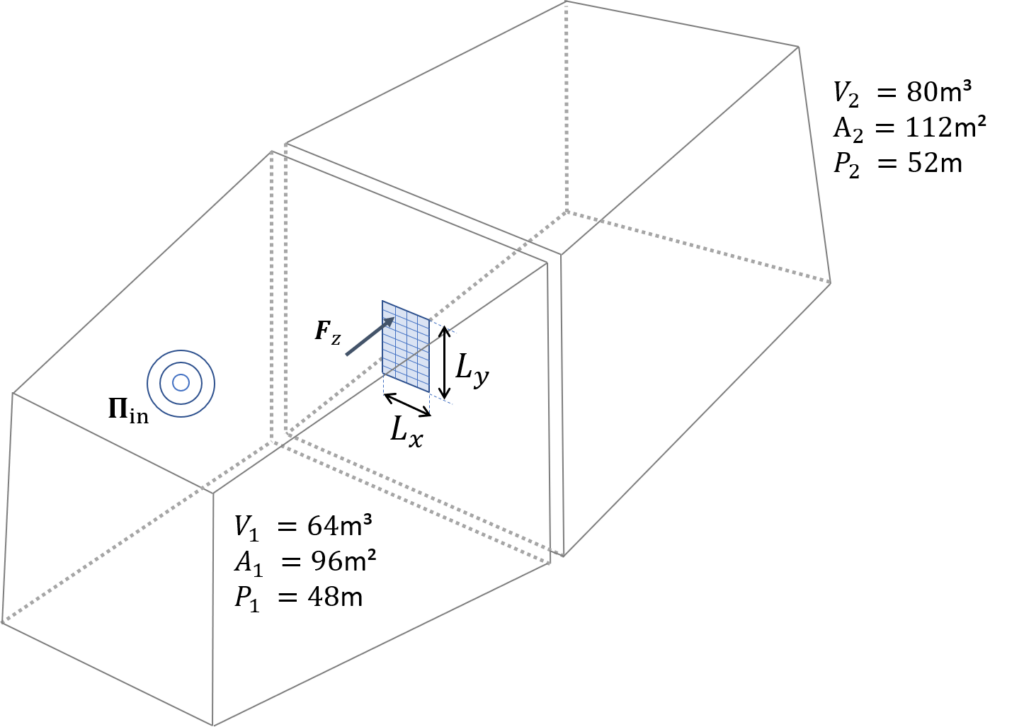
Hybrid FEM/SEA model case of a twin chamber configuration with tow reverberant rooms and a panel under test. — **Figure:** The twin chamber as hybrid FEM/SEA model with force and power source.

The two sources are treated in separate cases:

Literature

From my former work in the field of hybrid FEM/SEA and statistical energy analysis as far as combining all methods there are some papers worth reading…

[1] A. Peiffer, C. Moeser, and A. Röder, Transmission loss modelling of double wall structures using hybrid FEM/SEA simulation, in Fortschritte der Akustik, Merano, Mar. 2013, pp. 1161–1162.

[2] A. Peiffer, Hybrid (FEM/SEA) modelling of transmission loss with acoustic treatment, in Fortschritte der Akustik, München, Germany, Mar. 2018, pp. 50–53.

[3] A. Peiffer and S. Tewes, Hybrid FEM/SEA model of an aircraft fuselage section, in NAG/DAGA International Conference on Acoustics 2009, Rotterdam, The Netherlands, Mar. 2009, p. 3.