Deterministic Methods (FEM)

Deterministic methods apply at low frequencies where the wave propagation through fluids and structures is given by wavelengths similar to the size of the system. Small variations and changing environmental conditions lead to relatively small changes of the wave pattern in the systems. In this case we say the dynamic system is deterministic.

In a statistical thought experiment this means that if we take an ensemble of dynamic systems we will always get nearly the same response for all members of the ensemble.

Deterministic methods implementation

In a deterministic system the wave motion is calculated for every degree of freedom that is required to calculate the dynamic response. In many cases this is done by the finite element method (FEM). This is the reason why deterministic system are often called FEM-systems. However, a deterministic behavior can be calculated by many other methods, e.g. boundary element or – for simple systems – also by analytical solutions.

\begin{bmatrix} \bm D \end{bmatrix}
\begin{Bmatrix} \bm q \end{Bmatrix} = \begin{Bmatrix} \bm F \end{Bmatrix}

With and being the generalized coordinates and forces, respectively. is the stiffness matrix. In case of large models the number of degrees of freedom can become huge requiring huge matrices that need high memory and computational power.

An advantage of deterministic methods is that the model represents well the real system. The result is in real physical coordinates as for example velocity or pressure.

The book is not about finite element methods, but for the use in hybrid FEM/SEA models, a basic knowledge on finite elements models is mandatory.

Simulation results

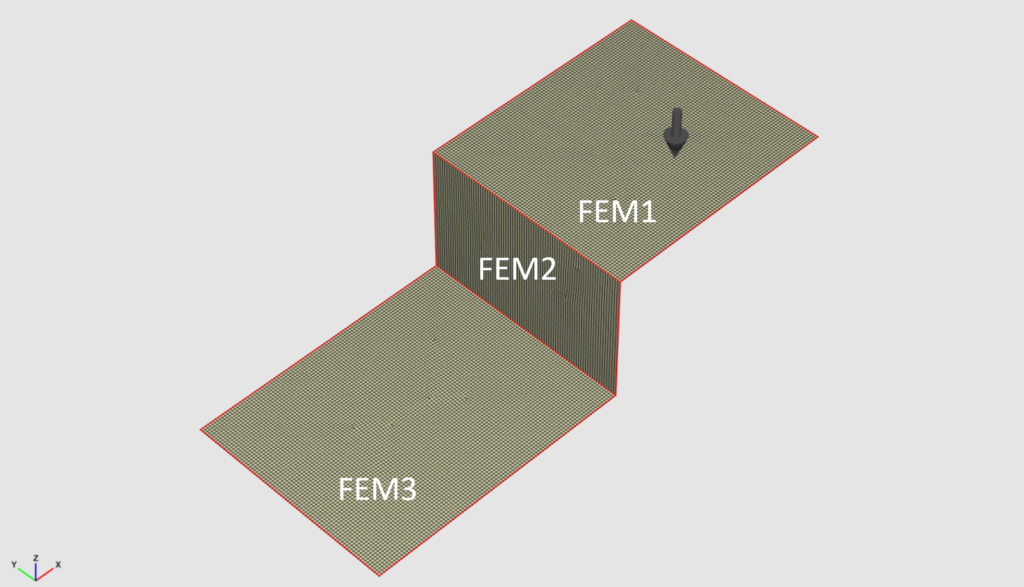
A typical frequency response of the three plate configuration is shown in the following figure. We can clearly identify the resonances in the response function. Small changes will lead to similar response graphs.

Deterministic examples

My book is not a book about finite element methods (FEM). There are a lot of reference books on this subject. However, in order to present principle concepts of deterministic modelling fluid and structure systems are modeled by deterministic methods in chapter 3 and 4, for example as analytical equations and modal analysis.

Those derivations provide important information about the systems that are also needed for the random description of such systems. In addition in chapter 9 deterministic applications are presented, such as acoustic one dimensional networks and infinite layer models based on transfer matrix theory. The latter is very useful to calculate the effect of noise control treatments in statistical energy analysis models.

In pyva there are some worked out deterministic examples that can also be used in the design of acoustic ventilation or muffler systems.

• The expansion chamber
• Helmholtz resonator in pipe