SEA Area Junctions - Alexander Peiffer

Introduction

Area Junctions are special in SEA theory. For cavity-plate-cavity connections there are not only direct paths. This violates the principle SEA assumption that only connected subsystems can exchange energy

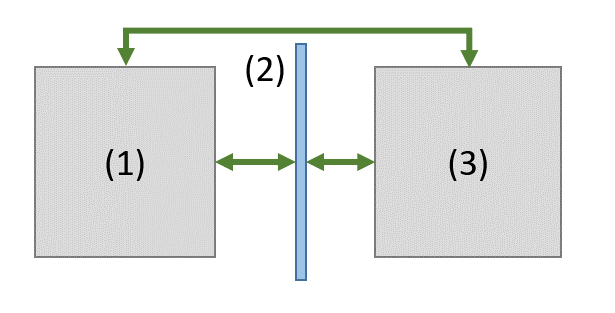
Two cavity systems connected via a plate system and transfer paths of SEA coupling — **Figure:** Area junction of cavity-plate-cavity connection

An intrusive way to understand the different paths is the transmission formula from Cremer.

\tau(\vartheta) = \left[ \left( \frac{m''\omega}{\rho_0c_0}\right)^2 \{\frac{k_a^4\sin^4\vartheta}{k_B^4}-1\}^2 \cos^2\vartheta+1\right]^{-1}

$m'', \rho_0$ and $c_0$ are mass per area, fluid density and speed of sound, respectively. $k_a$ and $k_B$ are the cavity air and plate bending wavenumber. $\vartheta$ is the angle of the incoming wave to the plate normal.

The $\frac{k_a^4\sin^4\vartheta}{k_B^4}$ term represents the two paths going through the bending wave field of the plate. As this are the paths that connect the wave field of the plate with the reverberant field of the cavity those paths are called the resonant paths. The plate resonates and retains energy.

The $1$ correspond to the direct path connection between both cavities. Better known as mass law and called the non-resonant path in the SEA theory. The plate experiences a forced motion and no energy is retained in the plate

Resonant Coupling Loss Factor

How is the resonant coupling loss factor (CLF) calculated? It is common practice to apply the radiation efficiency $\sigma$ .

\eta_{21} = \frac{\rho_0c_0}{m''\omega}\sigma

The formula is simple – the devil is in the calculation of the radiation efficiency, which is not that easy. Details are given in section 8.2.3.4 of my book.

Non-resonant Couling Loss Factor

The non-resonant coupling loss factor is calculated from the mass-law transmission coefficient $\tau_{mass}$ . CLF and transmission coefficient are related for 2D couplings by:

\eta_{13} = \frac{k_a^2 S_j\tau_{mass}}{8\pi^2n_1(\omega)\omega}

Twin chamber example

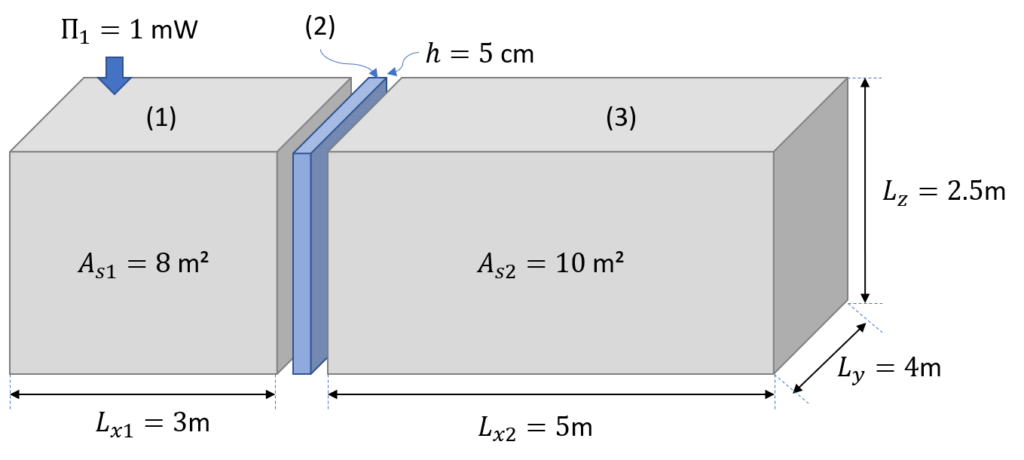
Example of an SEA model of two rooms separated by a concrete wall — **Figure:** Two room cavities separated by a concrete wall

The example is described in detail in the pyva documentation. The result is the TL of the wall is shown as follows. You may guess which kind of material and wall we have here…

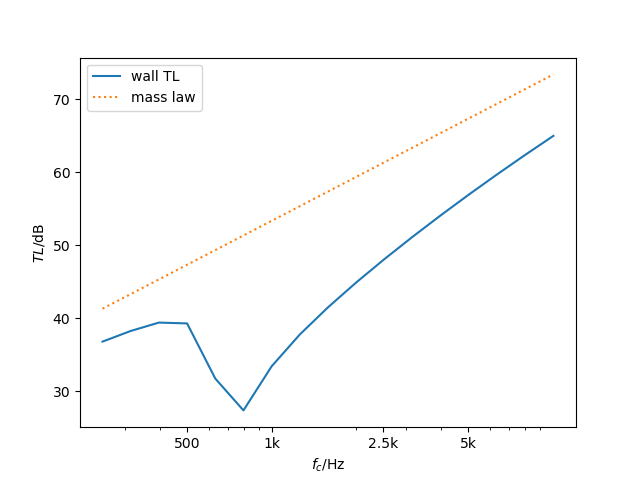
Two curves showing the transmission loss of the concrete wall. One without (dotted red) and on with the resonant transmission. — **Figure:** Transmission loss of concrete wall and limp wall of same mass.

One big advantage of SEA is, that contribution of each path can be monitored in detail. The following figure shows why concrete walls are not always a good idea (especially when very thin) in modern Buildings. The excellent radiation efficiency of the concrete wall transmits the acoustic power too well.

Introduction

Resonant Coupling Loss Factor

Non-resonant Couling Loss Factor

Twin chamber example

Leave a Comment Cancel Reply