Statistical Energy Analysis (SEA)

Statistical energy analysis is used when the wavelength in vibroacoustic systems becomes much smaller than the dimension of the system. In this case small changes have strong impact on the dynamic response of the system. The systems become random and this usually happens for high frequencies. Such systems are called dynamically complex.

As a consequence statistic methods are needed to model such a system. In contrast to deterministic methods where a fixed amplitude and phase response can be calculated this is not possible (and reasonable) for random systems. One model conception to deal with this subject is to describe such a system by multiple reflected waves with random phase – this wave field is called a (random) reverberant wave field.

Statistical energy analysis from ensemble averaging

In order to understand how random dynamic systems are modeled it is helpful to consider an ensemble of similar systems. Those systems have small variation of properties such as material properties, shape, thickness, size, etc.

**Figure:** Visualization of an ensemble of similar complex systems

In a Monte Carlo analysis we calculate the response of each system and perform specific average operations to understand the consequences of the random behavior.

Mean value of the ensemble …

Figure showing the mean value of an ensemble of dynamic systems — **Figure:** Expected mean value of a ensemble of complex dynamic systems

$\Psi_i$ is the wave quantity, for example the displacement. For the statistical evaluation we use the expected mean value:

\langle{\bm \Psi(r)}\rangle=\lim_{M\to\infty}\frac{1}{M}\sum_{i=1}^M{\bm\Psi(r)}

In a perfect random reverberant wave field the result is zero, except the direct fields of sources radiating into the subsystem.

Mean square value

When we calculate the mean square value:

\langle\bm\Psi(r)\bm\Psi(r)^*\rangle=\lim_{M\to\infty}\frac{1}{M}\sum_{i=1}^M{\bm\Psi(r)\bm\Psi(r)^*}

we get both, the averaged square wave quantity of the reverberant and the direct field.The result in a perfect reverberant field would be nearly constant over system extension.

A dynamically complex system can be described by a reverberant field characterized by the mean square value of the wave amplitude.

Energy flow

In statistical energy analysis the averaged response is provided by mean square response quantities such as pressure or velocity. Due to the fact that the squared value of those quantities correspond to energy this method is called statistical energy analysis.

In each real system there is dissipation. This dissipation is given by the damping loss. Every $m$ th system with energy $E_m$ dissipates the power $\Pi^{(m)}_{diss}$ at frequency $\omega$ :

\Pi^{(m)}_{diss}=\omega\eta_m E_m

When two random subsystems are connected they exchange energy. The power flow $\Pi_{mn}$ from the $m$ th system to the $n$ th system is given in accordance to the damping loss factor by the coupling loss factor $\eta_{mn}$ :

\Pi_{mn}=\omega\eta_{mn}E_m

The calculation of the coupling loss factor is a complicated task, because it must consider all aspects of the wave transmission and conversion at the system connections also called junctions.

Energy is introduced into each subsystem by external sources for example point forces or sound sources with resulting input power $\Pi^{(m)}_{in}$ . Summing up all this the power flow in a two system SEA model has the power balance as shown in the following figure.

Sketch of two SEA systems and their related energy flow — **Figure:** Two subsystem statistical energy analysis model

The power equation of a more complex SEA model of N systems would be given as:

\omega \begin{bmatrix} \eta_1+\sum_{n\ne 1}^{N}\eta_{1n} & -\eta_{21} & \cdots & -\eta_{N1}\\ -\eta_{12} & \eta_2+\sum_{n\ne 2}^{N}\eta_{2n} & & \vdots \\ \vdots & & \ddots & \\ -\eta_{1N} & \cdots & & \eta_N +\sum_{n\ne N}^{N}\eta_{Nn} \end{bmatrix} \begin{Bmatrix} E_1\\ E_2 \\\vdots \\ E_N \end{Bmatrix} = \begin{Bmatrix} \Pi_{\rm in}^{(1)}\\ \Pi_{\rm in}^{(2)} \\ \vdots \\ \Pi_{\rm in}^{(N)} \end{Bmatrix}

The matrix is called the SEA- or power flow matrix of the SEA model.

Symmetric version and flow analogy

With the modal density $n_m(\omega)$ of each subsystem the SEA matrix can be written in symmetric form.

\omega \begin{bmatrix} n_1 \sum_{n=1}^{N} \eta_{1n} & -n_2(\omega)\eta_{21} & \cdots & -n_N(\omega)\eta_{N1} \\ -n_1(\omega)\eta_{12} & n_2 \sum_{n=1}^{N} \eta_{2n} & & \vdots \\ \vdots & & \ddots & \\ -n_1(\omega)\eta_{1N} & \cdots & & n_N \sum_{n=1}^{N} \eta_{Nn} \end{bmatrix} \begin{Bmatrix} \frac{E_1}{n_1(\omega)} \\ \frac{E_2}{n_2(\omega)} \\ \vdots \\ \frac{E_N}{n_N(\omega)} \end{Bmatrix} = \begin{Bmatrix} \Pi_1(\omega) \\ \Pi_2(\omega) \\ \vdots \\ \Pi_N(\omega) \end{Bmatrix}

In the literature SEA if often visualized by a fluid basin analogy.

Water tanks showing the principle of the fluid analogy of SEA — **Figure:** Fluid analogy of statistical energy analysis

A detailed Monte Carlo Study on academic systems (plates, cavities) and theory of random systems is described in chapter 6 of my book. Chapter 8 goes into the details of coupling loss factor calculations.

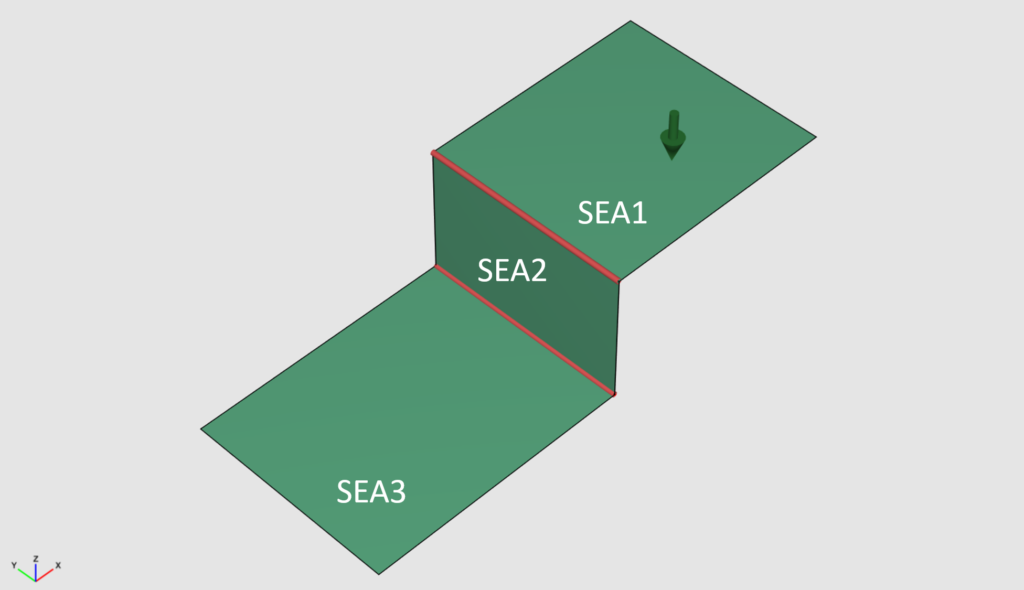
Result of the three plate example

In the following figure the space averaged root mean square velocity of all three plates due to unit input power at the point source is shown . The peaky shape at low frequencies in the deterministic method range can be easily identified. The first plate (where the energy is introduced) agreed very well even in mid frequency. It is obvious that statistical energy analysis will fail at low frequencies.

In the high frequency range the FEM curves are become jagged but very near to the SEA result. This is the frequency range where random methods can be applied.

Note that there is no ensemble average applied. Thus, for simple academic system SEA works on one subsystem when the space averaged system responses are used.

Figure: SEA and FEM results of the subsystems

Examples of SEA simulations

In my book you find worked out examples in chapter 6 such as:

Twin chamber configuration according to ISO 10140-2
Coupled plates
Twin chamber built out of concrete walls
Plate with noise control treatment
Box cover for sources without and with different treatment

As all theory is useless the text case can be followed in slightly different version using pyva. Here complete code examples are given in the SEA model examples section. Those examples are:

Literature

[1] A. Peiffer, S. Tewes, and S. Brühl, SEA Modellierung von Doppelwandstrukturen (statistical energy analysis implementation of double wall junctions) in Fortschritte der Akustik, Stuttgart, Germany, Mar. 2007.

[2] A. Peiffer and Z. Wang, SEA Simulation einer Flugzeugseitenwand und Korrelation zu Testdaten, in Fortschritte der Akustik, Nürnberg, Germany, Apr. 2015, p. 4.